Le scale di Magnitudo di un terremoto

I moderni sismografi amplificano e registrano con precisione il movimento del suolo  (tipicamente con periodi compresi tra 0.1 e 100 secondi) in funzione del tempo, sotto forma di ampiezze e tempi di arrivo delle onde sismiche per terremoti vicini e lontani. Sebbene sismografi siano esistiti fin dal 1890, fu solo nel 1930 che Charles F. Richter, un sismologo Californiano, ha introdotto il concetto di Magnitudo di un terremoto. La sua definizione originale valeva solo per i terremoti della California che si verificano entro 600 km di un particolare tipo di sismografo (lo strumento di torsione Woods-Anderson). La sua idea di base era molto semplice: conoscendo la distanza sismografo – ipocentro e osservando l’ampiezza massima del segnale registrato sul sismografo, era possibile dare un ranking quantitativo empirico della dimensione inerente al terremoto o meglio della sua energia. La maggior parte dei terremoti della California si manifestano entro i primi 16 km della crosta, in prima approssimazione, quindi non erano necessarie  correzioni per variazioni della profondità focale di un terremoto.

La Scala di magnitudo originale di Richter (M_L) è stata poi estesa alle osservazioni di terremoti di qualsiasi distanza e di profondità focali comprese tra 0 e 700 km. Poiché i terremoti producono due tipi di onde, onde di volume (P e S), che viaggiano all’interno della Terra, e onde superficiali (L e R), che sono costrette a seguire le guida d’onda naturali degli strati più superficiali della Terra, si sono evolute due nuove scale di magnitudo – le m_b (body waves) e le M_S (surface waves).

La “magnitudo” di un terremoto è una grandezza che si rapporta con la quantità di energia trasportata da un’onda sismica e viene calcolata sulla base di misure effettuate sul sismogramma (massima ampiezza di oscillazione e stima della distanza dall’epicentro di quella stazione sismografica). 
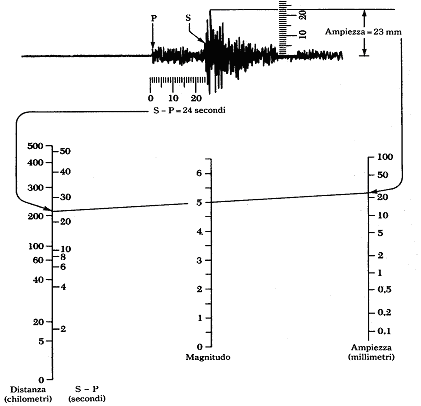
Richter definì con magnitudo M=0 un terremoto che, a una distanza dall’epicentro di 100 Km della stazione di riferimento, genera una traccia sul sismogramma dell’ampiezza di 1 micron. Stabilì poi di attribuire la magnitudo M=1, M=2, ecc. a quel terremoto che, alla stessa distanza, causa un’ampiezza di oscillazione 10, 100, ecc. volte superiore a quella del terremoto di magnitudo M=0

 La formula della Magnitudo standard per le onde di volume è:

 m_b = log₁₀ (A / T) + Q (D, h)

 dove A è l’ampiezza del movimento del suolo (in micron), T è il periodo corrispondente (in secondi) e Q (D, h) è un fattore di correzione che è funzione della distanza D (gradi), tra epicentro e stazione e profondità focale, h (in chilometri), del terremoto.

 La formula standard per il calcolo della Magnitudo delle onde superficiali è:

 M_S = log₁₀ (A / T) + 1.66 log₁₀ (D) + 3.30

 Ci sono molte varianti di queste formule che tengono conto degli effetti di specifiche regioni geografiche, in modo che la grandezza calcolata finale sia ragionevolmente coerente con la definizione originale di Richter di M_L. I valori di magnitudo negativi sono consentiti.

Per la scala m_b si usano in genere ampiezze delle onde compressive P di 1 secondo. La scala M_S utilizza onde superficiali di Raileigh nel range di periodo T = 18-22 s .

 Quando inizialmente sviluppate, queste scale di grandezza erano state considerate equivalenti  in altre parole, i terremoti di tutte le dimensioni si pensava che irradiassero proporzioni fisse di energia a periodi (T) differenti. Ma poi si è scoperto che i terremoti più grandi, con superfici di rottura più grandi, irradiano sistematicamente più energia di lungo periodo. Quindi, per terremoti molto grandi, le magnitudo delle onde di volume (P e S) sottostimavano parecchio la  vera dimensione del terremoto; le massime magnitudo delle onde di volume erano infatti di circa 6.5-6.8. Anche le magnitudo delle onde superficiali sottostimavano la dimensione di terremoti molto grandi, i valori massimi osservati erano circa di 8.3-8.7. Alcuni ricercatori hanno suggerito che le onde Love di 100 s (altro tipo di onde superficiali come le Raleigh) dovrebbero essere utilizzate per stimare la magnitudo dei grandi terremoti. Tuttavia, anche questo approccio non tiene conto del fatto che il danno alla struttura è spesso causato da energia a periodi più corti (alte frequenze). Così, i sismologi moderni si rivolgono sempre più a due parametri separati per descrivere gli effetti fisici di un terremoto : momento sismico ed energia irradiata.

Geometria della Faglia e Momento Sismico M_O

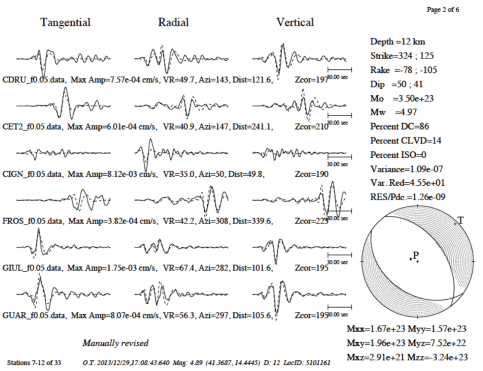
L’orientamento della faglia, la direzione di movimento della faglia e la dimensione di un terremoto possono essere descritti dalla geometria della faglia e dal momento sismico. Questi parametri sono determinati dalle analisi di forme d’onda dei sismogrammi prodotte da un terremoto. Il momento sismico è legato ai parametri fondamentali del processo di fagliazione 

M_O = μ S <d>

 dove μ è la resistenza al taglio della roccia fratturata , S è l’ area della faglia , e <d> è l’entità della dislocazione media sulla faglia, cioè di quanto le parti a contatto si sono spostate tra loro relativamente. 

E’ stata quindi definita una nuova scala di magnitudo Mw, detta magnitudo momento, che non va in saturazione

M_w = 2/3 log₁₀ (M_O) – 10.7 

 I due più grandi momenti sismici associati a terremoti segnalati sono 2.5 X 10³⁰ dyn·cm per il terremoto del Cile del 1960 (M_S 8.5; M_w=9.6 ) e 7.5 X 10²⁹ dyn·cm per il terremoto dell’Alaska del 1964 (M_S 8.3; M_w 9.2).

 Energia – E –

La quantità di energia irradiata da un terremoto è una misura del potenziale dei danni alle strutture antropiche. Teoricamente, il suo calcolo richiede di sommare il flusso di energia per un ampio range di frequenze generate da un terremoto durante il processo di fagliamento. A causa delle limitazioni strumentali, storicamente la maggior parte delle stime di energia hanno fatto sempre affidamento sulla relazione empirica sviluppato da Beno Gutenberg e Charles Richter :

 Log₁₀E = 11.8 + 1.5 M_S

 in cui l’energia, E, è espresso in erg. Lo svantaggio di questo metodo è che M_S è calcolata da una ampiezza di banda tra circa 18 a 22 s. È ormai noto che l’energia irradiata da un terremoto è concentrato su una banda diversa e a frequenze più alte. Con la diffusione mondiale dei moderni sismografi a registrazione digitale che hanno responsi con ampie larghezze di banda, i metodi di calcolo sono ora in grado di effettuare stime precise ed esplicite di energia su routines di calcolo di base per tutti i grandi terremoti.  Una magnitudo basata su energia irradiata da un terremoto, M_e , ora può essere definita ,

 M_e = 2/3 Log₁₀E – 2.9

 Per ogni aumento di magnitudo di 1 unità , i relativi aumenti di energia sismica sono di circa 32 volte.

 Sebbene M_w and M_e sono entrambi magnitudo, esse descrivono diversi proprietà fisiche del terremoto. M_w, calcolata dai dati sismici a bassa frequenza, è una misura della zona fratturata di un terremoto; M_e , calcolata a partire dai dati sismici ad alta frequenza, è una misura del potenziale sismico dei danni. Di conseguenza, M_w e M_e spesso non hanno lo stesso valore numerico.

Può essere interessante e istruttivo analizzare il rapporto tra due eventi sismici, 1 e 2, come rapporto tra le corrispondenti energie in gioco, E₁ ed E₂, relazionate con le rispettive magnitudo, M₁ ed M₂. Infatti:

log E₂= 11.8 + 1.5 M₂     

log E₁ = 11.8 + 1.5 M₁

facendo la differenza:

log E₁ – log E₂ = 1.5 (M₁ – M₂), ovvero log E₁/E₂ = 1.5 (M₁ – M₂)

e quindi, ponendo M₁ – M₂ = Δ M

E₁/E₂ = 10^1.5 ΔM

vale a dire che, ad esempio:  

se ΔM = 1,   E₁/E₂ = 10^1.5 = 31.6

se ΔM = 2,  E₁/E₂ = 10³ = 1000

se ΔM = 3,  E1/E2 = 10^4.5 = 31600

se ΔM = 4,  E₁/E₂ = 10⁶ = 1000000 ecc.

In altre parole, un terremoto di magnitudo 5 rispetto ad un terremoto di magnitudo 4 (ΔM = 1) ha uno spostamento del suolo di 10 volte superiore, ma un’energia liberata e quindi potenzialità di creare danni di circa 30 volte (31.6) superiore. Un terremoto di M=5 rispetto ad uno di magnitudo M=3 (ΔM = 2)  ha una ampiezza di spostamento di 100 volte superiore ma un’energia liberata 1000 volte superiore e così via….

Raffaele Viola